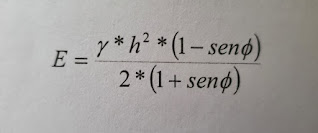Solicitaciones a considerar en los puentes - Fuerza centrífuga

 Cuando un puente está ubicado en una curva, se deberá tener cuidado de verificar la fuerza centrífuga que puede provocar momentos torsores importantes en la superestructura y esfuerzos cortantes a nivel de apoyos y coronamiento de la infraestructura.

Esta fuerza viene dada como un porcentaje de la carga viva sin impacto y se evalúa con la siguiente expresión:

Donde:

v = Velocidad de diseño de la carretera en Km./HR.

R = Radio de curvatura en el eje del puente en metros

La fuerza horizontal resultante por este concepto debe ser aplicada a todas las fajas de tráfico.

La altura de aplicación de esta fuerza es 1.8m. sobre la capa de rodadura.

En los puentes curvos se debe prever el peralte de la calzada evitando espesores adicionales, es decir alzando las vigas sobre sus pedestales de apoyo.

Cuando un piso de losa de hormigón armado o un tablero de parrilla metálica está ligado a sus apoyos, se puede suponer que el tablero resiste dentro de su plano el corte resultante de la fuerza centrífuga que transmite la carga viva, para lo que el peralte será tomado en cuenta.

Solicitaciones a considerar en los puentes - Fuerzas sísmicas

 En versiones pasadas de A.A.S.T.H.O. (Las actuales trabajan con la respuesta sísmica y lógicamente su aplicación viene acompañada del plano de Estados Unidos en general cuando se considera sismo en los puentes, la fuerza horizontal está dada por: 

Fh = C*D

Donde:

Fh = Fuerza horizontal aplicada en cualquier dirección y en el centro de gravedad de la estructura.

D = Carga muerta de la estructura.

C = 0.02 para estructuras en cuyo plano de fundación el terreno está sometido a presiones mayores a 0.4 MPa.

C = 0.04 para estructuras en cuyo plano de fundación el terreno está sometido a presiones inferiores a 0.4 MPa.

C = 0.06 para estructuras asentadas sobre pilotes o tubulones.

No se toma en consideración la carga viva.

Se recomienda tomar en este aspecto las normas para sísmicas de cada país, AASHTO las tiene apropiadas a USA.

Solicitaciones a considerar en los puentes - Fuerza de tierras

 Los estribos, además de recibir las reacciones transmitidas por la superestructura están sometidos al empuje de las tierras que conforman el terraplén de acceso para lo que se aplican las siguientes expresiones:

Cuando no hay Sobrecarga en el terraplén:

Cuando se considere carga viva distribuida sobre el terraplén se trabaja con una altura equivalente que es adicionada a la altura del relleno o sea:

Las presiones calculadas con las fórmulas anteriores no deben ser inferiores a las de un líquido equivalente con peso específico de 4.8 kN/m³, es decir:

Cuando los accesos llevan losa de hormigón armado adecuadamente diseñada y apoyada en el coronamiento del estribo no se considerará presión por carga viva.

De todas maneras, tantos estribos como aleros deben llevar drenajes consistentes en barbacanas (huecos que atraviesan los muros) o colectores con tubería perforada y relleno en un espesor de 0.3 m detrás del muro con material granular graduado a manera de filtro.

Solicitaciones a considerar en los puentes - Fuerza de la corriente

 Las aguas provocan una fuerza con tendencia a volcar particularmente las pilas por ello estas deben ofrecer la menor resistencia posible, lo que se consigue dándole formas hidrodinámicas y lo que es más ubicando la pila con la menor sección en la dirección de la corriente y es por ello según se puede observar en la figura 37 que los puentes frecuentemente son enviajados y la infraestructura debe ofrecer la mejor resistencia al paso de la corriente de agua.

Donde: 

p = Presión de la corriente en kN/m²

v = Velocidad de las aguas en m/seg

K = Constante cuyos valors se deducen de la figura 38

Solicitaciones a considerar en los puentes - Fuerza de levantamiento

 Se tomarán providencias para la unión de la superestructura con la infraestructura cuando una carga o combinación de cargas incrementadas al 100 % de la carga viva mas impacto provoque fuerzas de levantamiento en cualquier apoyo (ocurre cuando un tramo interior es demasiado grande en relación a tramos extremos muy cortos apareciendo componentes de reacción que levantan y en realidad golpetean, fenómeno conocido como fatiga y que se traduce en un deterioro del pedestal de apoyo).

Solicitaciones a considerar en los puentes - Viento en la infraestructura

 Además de las reacciones por viento transmitidas por la superestructura se tomará una presión de 2 kN/m² aplicada en la dirección más desfavorable para lo que luego de su aplicación se la descompone en las dos direcciones antes mencionadas.

En la figura 36 se muestra la dirección más desfavorable del viento sobre una pila, de manera que las fuerzas resultantes por este concepto son respectivamente:

Viento longitudinal:

Donde: 

p = Presión del viento en la infraestructura 

P = 2 kN/m²

L = Separación entre ejes de pilas en metros

D = Ancho de la pila en metros

B = Espesor de la pila en metros

H = Altura libre de la pila entre el nivel de aguas y su coronamiento en metros.

Las unidades para Fvl y Fvt serán en kilo Newton (kN)

Solicitaciones a considerar en los puentes - Viento en la carga viva

 Será considerada como una fuerza por metro lineal de estructura de acuerdo a la tabla siguiente:

Estas cargas se aplican a 1.8m por encima de la capa de rodadura.

En puentes corrientes con luces de hasta 50 m se emplearán las siguientes cargas:

• Viento longitudinal sobre la carga viva: 0.06 kN/m
• Viento transversal sobre la carga viva: 1.50 kN/m

Estas presiones se aplican a la misma luz de cálculo en los dos casos.